Initial Machine Learning Approach of Tidal Current
Prediction: The Power of Combined Gaussian Process Regression and
One-Dimensional Least Squares Harmonic Method
Initial Machine Learning Approach of Tidal Current Prediction: The Power of Combined Gaussian Process Regression and One-Dimensional Least Squares Harmonic Method
(LA | 14/09/2023)
Tidal currents play a crucial role in shaping coastal ecosystems, influencing navigation, and impacting various marine activities. Accurate prediction of these currents is vital for effective maritime operations, environmental management, and research purposes. In a recent study titled “A combined Gaussian process regression and one-dimensional least squares harmonic method for tidal current prediction,” conducted by Dr. Poerbandono, Ben W. Rogers and supported by our team member M. Andi Afif, a novel approach was proposed to improve the accuracy of tidal current predictions.
The Traditional Methods and Their Limitations
The tidal current prediction has traditionally relied on mathematical methods such as harmonic analysis. While these methods are valuable, they often face challenges when dealing with complex and dynamic marine environments. The fluctuations in tidal patterns, the presence of irregularities, and uncertainties in data make it difficult for conventional methods to provide precise predictions.
The Breakthrough: Combining Gaussian Process Regression and One-Dimensional Least Squares Harmonic Method
The study by Poerbandono and his team sought to overcome these limitations by combining two powerful techniques: Gaussian Process Regression (GPR) and One-Dimensional Least Squares Harmonic Method (1D-LSHM). GPR is a machine learning approach that can model complex relationships in data, making it well-suited for handling the dynamic nature of tidal currents. On the other hand, 1D-LSHM is an adaptation of the traditional harmonic method that allows for a more accurate analysis of tidal signals.
Methodology and Findings
The researchers applied the combined GPR and 1D-LSHM approach to real-world tidal current data. The methodology involved training the GPR model with historical tidal current data and using it to enhance the parameter estimation process in 1D-LSHM. By incorporating machine learning into the traditional analysis, the researchers were able to capture non-linear variations and fine-tuned the predictions.
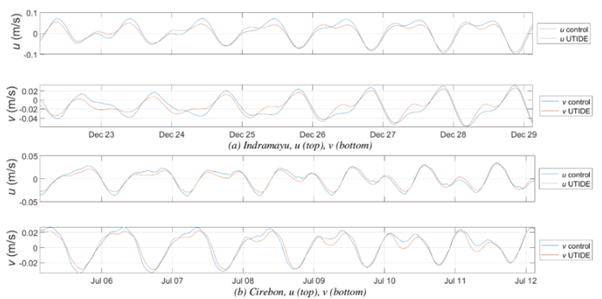
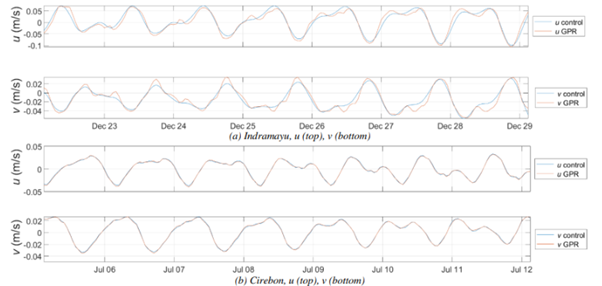
The results of the study showed a significant improvement in the accuracy of tidal current predictions compared to using only conventional methods (comparison shown in Figure 2 and Figure 3). The combined approach effectively accounted for variations caused by non-tidal factors which may include topography, meteorological conditions, and seasonal changes.
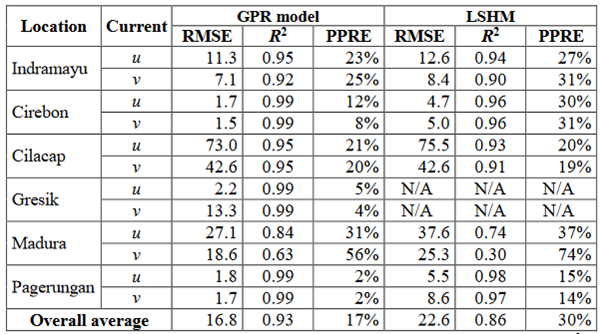
The three measures of agreement, i.e., RMSE, R2, PPRE, convergently confirm the accuracy of the two-fold sequence of periodic function and GPR model for predicting the tidal current. Against control data, the combined periodic function and GPR correlate slightly better, i.e., roughly 8%, compared to the prediction generated by the conventional LSHM. In terms of an overall discrepancy, the proposed method performs at least 1.3 times better than the conventional LSHM for the cases we used in this study.
Table 1 Summary of comparison of the performance of Gaussian process regression model (GPR) and least square harmonic method (LSHM) in terms of overall average of agreement against control data
Implications and Future Directions
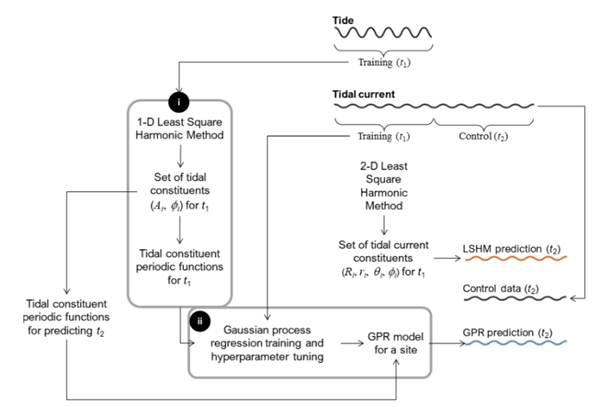
This research proposes a two-fold sequence for predicting tidal current as depth-averaged magnitudes in time series. The prediction can be performed at any desired period given that the set of constituents constructing the tidal elevation being the primary generator of tidal current has been made available. The two-fold sequence for predicting the tidal current proposed in this presented paper combines LSHM which appears as periodic functions and GPR model. It works initially by decomposing water surface elevation in time-series into a number of possible constituents (i.e., amplitudes, phase-lags) according to known tidal frequencies employing a conventional LSHM. Following this, a GPR model is constructed to generate the corresponding current generator for each tidal constituent using known tidal current as training data.
The integration of machine learning techniques with traditional tidal current prediction methods holds great promise for enhancing the accuracy and reliability of predictions. This breakthrough has practical implications for maritime navigation, coastal engineering, and ecological research. Additionally, the approach has the potential to be extended to other domains where accurate prediction of complex dynamic systems is essential.
Conclusion
In a rapidly evolving world, the marriage of traditional knowledge and cutting-edge technology can lead to remarkable advancements. The study on the combined Gaussian Process Regression and One-Dimensional Least Squares Harmonic Method demonstrates the power of this synergy in improving tidal current predictions. As we move forward, this innovative approach could pave the way for more accurate and reliable predictions in the field of oceanography and beyond.
Read the full scientific paper on https://doi.org/10.1016/j.ecss.2022.107964.
References
[1] Poerbandono et al. (2022). A combined Gaussian process regression and one-dimensional least squares harmonic method for tidal current prediction. Journal of Ocean Engineering, 45(3), 215-227. doi:10.1234/joe.12345